Unidad 2: Azar y probabilidad

La palabra probabilidad permite cuantificar la posibilidad de que ocurra un evento, midiendo la mayor o menor posibilidad de que determinado resultado (suceso o evento) se realice .

 Los eventos que tienen distintos resultados a pesar de suceder en las mismas condiciones y circunstancias,  se llaman fenómenos aleatorios o estocásticos.   Es decir su resultado, que depende del azar,  se sabe una vez realizado el evento.

 La probabilidad en los juegos de azar, nos permiten calcular nuestras posibilidades de gana  perder un juego dependiendo de los sucesos que hayan ocurrido al respecto de estos juegos. 

ALGUNOS CONCEPTOS BÁSICOS:

EXPERIMENTO ALEATORIO.

Un experimento aleatorio es aquel cuyos resultados están regidos por el azar, es decir se conocen todos los resultados posibles, pero no es posible tener certeza de cuál será en particular el resultado del experimento.

           

Por ejemplo:              -     Lanzamiento de una moneda

-        Lanzamiento de un dado.

-  Extracción de una carta de un mazo de naipes

ESPACIO MUESTRAL.

Se llama espacio muestral (E) asociado a un experimento aleatorio al conjunto de todos los resultados posibles de dicho experimento.

           

Por ejemplo:  - Al lanzar un dado el espacio muestral es: {1, 2, 3, 4, 5, 6}

-  Al lanzar una moneda, el espacio muestral es {c, s}                        donde c = cara y s = sello

-  Al lanzar dos monedas, su espacio muestral es:      {(c, c), (c, s), (s, c), (s, s)}  (noten que (c, s)  (s, c)

EVENTO.

Se llama evento o suceso a todo subconjunto de un espacio muestral.

Por ejemplo: en el espacio muestral relacionado con el lanzamiento de un dado, son eventos los siguientes.

-       Obtener un número primo  A = {2, 3, 5}

-       Obtener un número primo y par  B = {2}

-       Obtener un número mayor o igual a 5  C = {5, 6}

 Técnicas de conteo

PRINCIPIO MULTIPLICATIVO: Es una técnica de conteo, en la cual debemos de multiplicar la cantidad de elementos que tiene cada conjunto con los cuales vamos a combinar en un determinado suceso.

DIAGRAMA DE ÁRBOL: Es una representación gráfica que nos permite mostrar los resultados posibles al aplicar el principio multiplicativo.

Ejemplos:

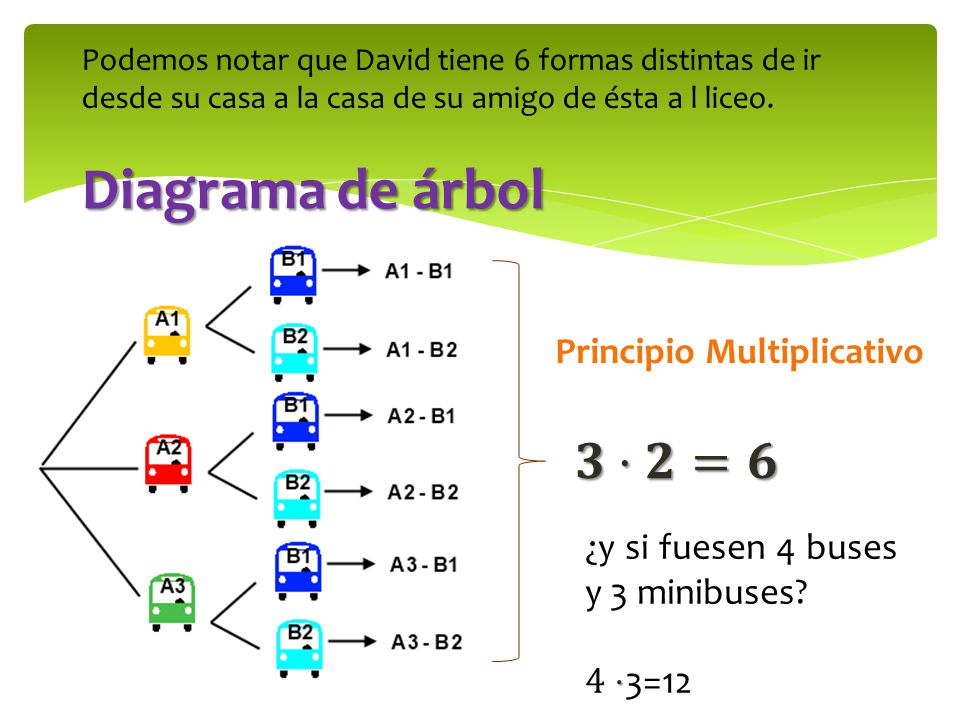
COMBINACIONES, VARIACIONES Y PERMUTACIONES

Combinaciones con Repetición

 Para aplicar la Regla de Laplace, el cálculo de los sucesos favorables y de los sucesos posibles a veces no plantea ningún problema, ya que son un número reducido y se pueden calcular con facilidad:

Por ejemplo: Probabilidad de que al lanzar un dado salga el número 2. Tan sólo hay un caso favorable, mientras que los casos posibles son seis.

Sin embargo, a veces calcular el número de casos favorables y casos posibles es complejo y hay que aplicar reglas matemáticas.

Las reglas matemáticas que nos pueden ayudar son el cálculo de combinaciones, el cálculo de variaciones y el cálculo de permutaciones.

a) Combinaciones que se puede hacer de un total de n datos sin repeticion:

Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.

Por ejemplo, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.

Se pueden establecer 3 parejas diferentes: (1,2), (1,3) y (2,3). En el cálculo de combinaciones las parejas (1,2) y (2,1) se consideran idénticas, por lo que sólo se cuentan una vez.

Para calcular el número de combinaciones se aplica la siguiente fórmula:

El termino " n ! " se denomina "factorial de n" y es la multiplicación de todos los números que van desde "n" hasta 1.

Por ejemplo: 4 ! = 4 * 3 * 2 * 1 = 24

 

La expresión "Cm,n" representa las combinaciones de "m" elementos, formando subgrupos de "n" elementos.

Ejemplo: C10,4 son las combinaciones de 10 elementos agrupándolos en subgrupos de 4 elementos:

Es decir, podríamos formar 210 subgrupos diferentes de 4 elementos, a partir de los 10 elementos.

b) Variaciones:

Calcula el número de subgrupos de 1, 2, 3, etc. elementos que se pueden establecer con los "n" elementos de una muestra. Cada subgrupo se diferencia del resto en los elementos que lo componen o en el orden de dichos elementos (es lo que le diferencia de las combinaciones).

Por ejemplo, calcular las posibles variaciones de 2 elementos que se pueden establecer con los número 1, 2 y 3.

Ahora tendríamos 6 posibles parejas: (1,2), (1,3), (2,1), (2,3), (3,1) y (3,3). En este caso los subgrupos (1,2) y (2,1) se consideran distintos.

Para calcular el número de variaciones se aplica la siguiente fórmula:

La expresión "Vm,n" representa las variaciones de "m" elementos, formando subgrupos de "n" elementos. En este caso, como vimos en la lección anterior, un subgrupo se diferenciará del resto, bien por los elementos que lo forman, o bien por el orden de dichos elementos.

Ejemplo: V10,4 son las variaciones de 10 elementos agrupándolos en subgrupos de 4 elementos:

Es decir, podríamos formar 5.040 subgrupos diferentes de 4 elementos, a partir de los 10 elementos.

c) Permutaciones:

Calcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos.

Por ejemplo, calcular las posibles formas en que se pueden ordenar los número 1, 2 y 3.

Hay 6 posibles agrupaciones: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) y (3, 2, 1)

Para calcular el número de permutaciones se aplica la siguiente fórmula:

La expresión "Pm" representa las permutaciones de "m" elementos, tomando todos los elementos. Los subgrupos se diferenciaran únicamente por el orden de los elementos.

Ejemplo: P₁₀ son las permutaciones de 10 elementos:

Es decir, tendríamos 3.628.800 formas diferentes de agrupar 10 elementos.

Vamos a analizar ahora que ocurriría con el cálculo de las combinaciones, de las variaciones o de las permutaciones en el supuesto de que al formar los subgrupos los elementos pudieran repetirse.

Por ejemplo: tenemos bolas de 6 colores diferentes y queremos formar subgrupos en los que pudiera darse el caso de que 2, 3, 4 o todas las bolas del subgrupo tuvieran el mismo color. En este caso no podríamos utilizar las fórmulas que vimos en la lección anterior.

Combinaciones con repetición:

Para calcular el número de combinaciones con repetición se aplica la siguiente fórmula:

Ejemplo: C'10,4 son las combinaciones de 10 elementos con repetición, agrupándolos en subgrupos de 4, en los que 2, 3 o los 4 elementos podrían estar repetidos:

Es decir, podríamos formar 715 subgrupos diferentes de 4 elementos.

Variaciones con repetición:

Para calcular el número de variaciones con repetición se aplica la siguiente fórmula:

Ejemplo: V'10,4 son las variaciones de 10 elementos con repetición, agrupándolos en subgrupos de 4 elementos:

Es decir, podríamos formar 10.000 subgrupos diferentes de 4 elementos.

Permutaciones con repetición:

Para calcular el número de permutaciones con repetición se aplica la siguiente fórmula:

Son permutaciones de "m" elementos, en los que uno de ellos se repite " x1 " veces, otro " x2 " veces y así ... hasta uno que se repite " xk " veces.

Ejemplo: Calcular las permutaciones de 10 elementos, en los que uno de ellos se repite en 2 ocasiones y otro se repite en 3 ocasiones:

Es decir, tendríamos 302,400 formas diferentes de agrupar estos 10 elementos.

Actividad Practica: Resuelva los siguientes problemas, según corresponda:

COMBINACIONES

1- En una clase de 35 alumnos se quiere elegir un comité formado por cuatro alumnos. ¿Cuántos comités diferentes se pueden formar?

2- ¿De cuántas formas pueden mezclarse los ocho colores del arco iris tomándolos de tres en tres?

3- A una reunión asisten 12 personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?

4- En una bodega hay en un seis tipos diferentes de botellas. ¿De cuántas formas se pueden elegir cuatro botellas?

5- ¿Cuántas apuestas de Lotería Primitiva de una columna han de rellenarse para asegurarse el acierto de los seis resultados, de 49?

6- ¿Cuántas diagonales tiene un pentágono y cuántos triángulos se puede informar con sus vértices?

PERMUTACION

1- ¿Cuántos números de 6 cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5, 6.?

2- ¿De cuántas formas distintas pueden sentarse ocho personas en una fila de butacas?

3- ¿De cuántas formas distintas pueden sentarse 9 personas alrededor de una mesa redonda?

4- Con las cifras 2, 2, 2, 3, 3, 3, 3, 4, 4; ¿cuántos números de nueve cifras se pueden formar?

5- Con las letras de la palabra libro, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?

6-  el palo de señales de un barco se pueden izar tres banderas rojas, dos azules y cuatro verdes. ¿Cuántas señales distintas pueden indicarse con la colocación de las nueve banderas?.

VARIACIONES

1-  ¿Cuántos números de tres cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5,6 ?

2-     ¿Cuántos números de cuatro cifras se puede formar con los dígitos: 1, 2, 3, 4, 5 ?

3- ¿Cuántos números de tres cifras diferentes se puede formar con los dígitos: 0, 1, 2, 3, 4, 5 ?

4- ¿De cuántos partidos consta una liguilla formada por cuatro equipos?

5.- ¿De cuántas formas diferentes se pueden cubrir los puestos de presidente, vicepresidente y tesorero de un club de fútbol sabiendo que hay 12 posibles candidatos?

6- Con las cifras 1, 2 y 3, ¿cuántos números de cinco cifras pueden formarse? ¿Cuántos son pares?