Unidad 1: Razones Trigonométricas en Triangulo Rectángulo

Trigonometría

La trigonometría es la rama de la matemática que relaciona la medida de los ángulos agudos en un triangulo rectángulo con razones entre los lados del mismo, dichas razones se conocen como Razones Trigonométricas.

Para identificar los lados de un triangulo rectángulo, debemos de tener en cuenta:

1- Hipotenusa:  es el lado mayor del triángulo, el lado opuesto al angulo recto (de 90°)

2- Cateto Opuesto: es el lado opuesto al ángulo, el lado que se encuentra al frente del angulo con que estamos trabajando.

3- Cateto Adyacente: es el lado adyacente al ángulo, el lado que se encuentra al lado del angulo con el que estamos trabajando.

Razones trigonométricas: 

 Debemos de calcular cada uno de las razones trigonométricas, dejando su resultado expresado en decimal, con dos decimales aproximados.

1- Si tenemos el valor de todos los lados: Aplicamos las formulas de las razones trigonométricas y luego dividimos.

Resultados: 

sen= 0,38 ;  tan= 0,42 ; sec= 1,08 ; cos= 0,92 ; cot=2,4 ; csc= 2,6

2- Si tenemos el valor de dos de los lados, aplicamos Teorema de Pitagoras para encontrar el tercer valor, luego aplicamos las formulas de razones trigonométricas y dividimos.

 resultados:
sen= 0,22;  cos= 0,98 ;  tan= 0,23;  csc= 4,56 ;  sec= 1,03 ;  cot= 4,44

Actividad Practica:  

I-  Calcule las razones trigonométricas sen, cos, tg, cosec, sec, cotg en cada uno de los triángulos, aplicando Teorema de Pitagoras, de ser necesario.

 Las razones trigonométricas, nos permiten calcular distancias y alturas en la vida cotidiana.

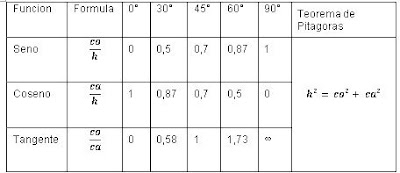
Para esto debemos de tener en cuenta los valores de las razones trigonométricas de los ángulos mas utilizados:

Ejemplo:
Encontraremos el diámetro desde tierra a la tabla de surf, siguiendo algunos pasos.

Primero, identificamos los lados del triangulo

Segundo, identificamos con que lados vamos a trabajar, en este cado CA = 8, 3 Y CO= X

Tercero, identificamos cual de las tres formulas nos sirve, en este caso Tangente = ca/co

Cuarto, reemplazamos los valores en la formula
Tg 60° = x / 8,3 m

Quinto, buscamos el valor del angulo en la tabla.

1,73 = x / 8,3 m

sexto, despejamos la incógnita

1,73 *  8,3 m = x
14,359 m =x
aproximando al segundo decimal

14,36 m es el diámetro desde tierra hasta la tabla de surf.

Act       Actividad Practica:
            II- Utilizar funciones trigonométricas para encontrar el valor de la incógnita de los ángulos básicos 

Para calcular otros ángulos debemos de utilizar la calculadora o una tabla de valores trigonométricas, como la que utiliza a continuación.

Ejemplo:  Calcularemos el valor de la incógnita, siguiendo los pasos del ejemplo pasado.

tg 37° =  21 /x +21

0,754 = 21 / (x +21)

0,754 (x +21) = 21

0,754 x + 15,834 = 21

0,754 x = 21 -15,834

0,754x = 5,166

x = 5166 / 0,754

x = 6,851 mts

Actividad Practica:  
III- Utilizar funciones trigonométricas para encontrar el valor de la incógnita de otros ángulos.

Actividad Practica:
IV- Investigación:
1- Biografía de quien descubrió las razones trigonométricas
2- Contexto histórico de donde fueron descubiertas
3- Explicar para que sirven las razones trigonométricas
4- Explicar tres hechos históricos donde utilizaron las razones trigonométricas en la historia. (ejemplo medir la tierra)
5- Explicar una utilidad actual de las razones trigonométricas en la vida cotidiana, con ejemplos.
6- Investigar sobre la utilización de goniometro para utilizar las razones trigonométricas. 
     - ¿como se construye uno artesanal?
     -  ¿Como funciona?
     - ¿Porque funciona?
      - mencionar un ejemplo

__________________________________________________________

Recuerdo: Teorema de Pitagoras